Blog

[dc]I[/dc] want to write what might be a complicated blog post, but stick with me. I’ll try to make it as clear as possible, because there is a good lesson here. Today, I want to look at volatility, how volatility evolves (changes), and how we can use that information: there is information here that is interesting to the outright directional trader, the volatility trader, and even long term portfolio managers who intend to do little, if any, active trading, so let’s dig in.

First, volatility is a bit difficult to understand because it cannot be measured directly. What is volatility? A precise academic answer is easy: volatility is the standard deviation of the return series, measured over some timeframe, and perhaps multiplied by a factor to annualize it. This is the classic historic volatility (also called statistical or realized volatility), but this simple definition may fail to capture some nuance. (This post, on how to calculate volatility in Excel, has been one of the most popular posts on this blog for quite some time, so this is a subject that is of interest to many traders.) There are other useful ways to measure volatility, such as the range of the price bars (or average true range, which is a standard technical tool), or by backing out volatility from the price of options or other derivatives. This last is implied volatility, which is important to options traders and options strategies. The factor that ties all of these measures of volatility together is that it is not as easily observed as price. July ’14 wheat futures are at 682 as I write this. I can see that by looking at the screen, but I would have to perform some calculations to tell you what the volatility of July ’14 wheat futures is. If you and I looked at different time periods (say weekly and quarterly) or different ways to measure that volatility, we would likely have very different answers. (Also, I can buy a lot of wheat and push the price up, or less and push it down. That is easy, but there exists no mechanism to influence the volatility of an asset that directly. And therein lies the source of many opportunities for savvy volatility traders, but that’s a topic for another day.)

Volatility is often thought of as measuring risk or uncertainty. We are never sure where an asset is going to be at some point in the future, but a more volatile asset will have a wider spread of likely ending values, compared to a less volatile asset for the same time period. In other words, if stock ABC and XYZ are both $50 stocks, but XYZ is much more volatile, and we had to guess where both of these $50 stocks would end up in a year, perhaps we would guess $45 – $55 as a likely range for ABC, but XYZ could reasonably be anywhere between $20 and $80. Again, we can dig a little deeper and find issues with the simple definition of volatility as risk (and this is a subject I covered in my book in some depth), but the core understanding—that a more volatile asset could cover a much wider range of prices—is important. Even with this, there is a problem.

Volatility changes. Today’s volatility may look nothing like tomorrow’s: something can happen to make even a quiet asset have a large change in price. This so-called volatility shock brings with it some other problems: volatility shocks tend to persist. In other words, when some piece of news makes an asset explode in volatility, that asset is likely to continue to be volatile in the future. If we want to understand how volatility evolves, this is an important part of that understanding: volatility shocks occur more or less randomly in assets (or broad markets), and these shocks tend to persist. This is well known, but there are a few other things to consider: volatility tends to trend in the short term, but this may be, over a large sample size, simply a reflection of that persistent and somewhat predictable decay of shocks. In the long-term, volatility tends to be mean reverting. For instance, no one thinks the VIX (a measure of implied volatility on stocks) is going to trend from 20 to 60 to 200 and keep going. Is it possible? Of course, literally anything is possible (and therein lie many of the profound and immeasurable market risks), but it is exceedingly unlikely for that to happen. Smart money does not place heavy bets on events like that, but mean reversion can also be problematic. Why? If the VIX (which, over the long haul tends to hang out somewhere around “18-sh” (that is precise market terminology there J) spikes up to 60, it is probably coming back to 20, but when? This month? Next year? Trading mean reversion is not trivial, even though it is a quantifiable factor in the long run.

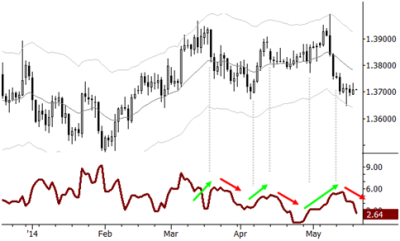
Take a look at the daily chart of the EURUSD with 7 (trading, not calendar) day historical plotted underneath. In the short-term volatility is trending, right? I’ve marked a few trends in recent volatility. Remember, volatility is calculated from price, so it lags price, but there is an important understanding here: Volatility expansion (volatility going up) is connected with trending price movements, and volatility contraction tends to be associated with consolidations. (Without getting too heavily into details, it’s also worth mentioning that we should not assume that trends = higher volatility. By some measures, volatility often decreases in trends. I picked a convenient example to illustrate the concept here, so I am not suggesting you trade directionally based on trends in the historical volatility. However, being able to read this aspect of price behavior is a critical part of the technical traders toolkit.) Notice the cycle: in consolidations, volatility contracts, almost as if the market is gathering energy, and then the market makes an explosive directional move. In time, that move exhausts itself, the market rolls over into a trading range (consolidation) and volatility begins to contract. The most fundamental technical cycle, the alternation of trend and trading range, is actually a cycle in the volatility of the asset!

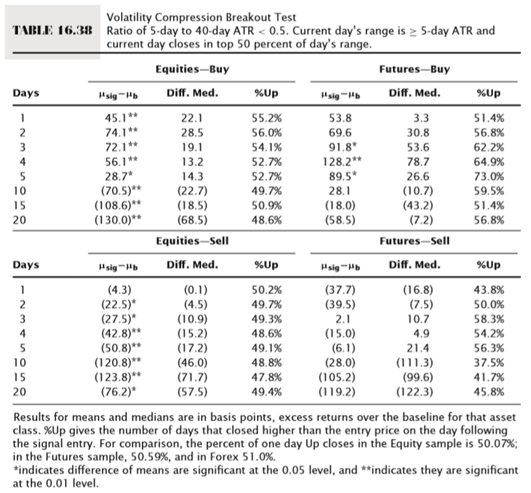
If you’re curious, the tendency for a sharp directional move to come after a volatility compression is a tradable tendency. There are many ways to define volatility compression, but this table from the unpublished portion of my book shows a test run on a very simple volatility compression system. Note strong short-term directional tendencies for stocks and commodities. (Volatility evolves a bit differently in currencies, so this system will call few or no currency trades.) If you don’t choose to trade a system like this, I would still suggest the lessons are important. Are you holding a rather quiet stock (sector, set of stocks, etc.) in your portfolio? What are you going to do if it has a large move against you, suddenly and out of the blue? (Volatility shock.) Many investors would hold it and hope things go “back to normal”, but, if you know these lessons, you will realize that a sharp move, up or down, is likely to continue for some time (the work in this table was done on daily bars, but can be repeated at much longer timeframes), and, at the very least, higher volatility is likely to persist for quite some time. Money is made, and money is protected, by placing smart bets with the odds, so you have to know how markets behave over a large sample size. Otherwise, we’re just guessing.

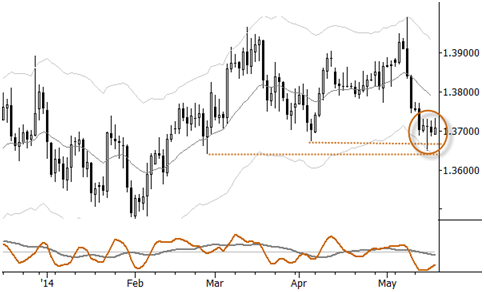
Now, take another look at the chart of the EURUSD, which is showing a consolidating (volatility contraction) sitting right on obvious support. This is not how a clean failure test should have resolved (absence of price rejection, if you are familiar with my other work), and the volatility compression should warn us that any sharp move is likely to see some continuation. This is how a market usually looks before it knifes through major support, and I would be very careful about buying breakdowns in this currency over the next few weeks. Of course, this call could end up being absurdly wrong, this time, but, over a large sample, smart money places smart bets with the statistical tendencies of the market place. You gotta know your stats.