Blog

This will be the last post in a short series in which we have looked at ways to quantify and to understand a trading edge. This series was motivated by a reader’s question, so here’s Anthony’s question again:

First, I was messing with the SPY up/down N-days and the returns N-days after. It was evident that returns were usually negative after consecutive up days, which makes sense because stocks tend to mean revert?? So I tried to do capitalize off that. For example, I had used SPY down 2 days in a row and the returns 5 and 20 days after. (assuming they would be positive and they were). However, the average return for 5 days was .06% (thats fine I guess) but the average return for 20 days was .41%. That made me skeptical. Seems to be good to be true! haha Is that the result of stocks statistically going “up”, was the number fudged somehow?

In the two previous posts in the series, we covered the following points:

• First, a simple (but oh so important) math lesson in which we look at how to calculate and “add” returns. This applies to both markets and trading accounts, and the takeaway is that you cannot add returns, you must compound them.
• Next, we looked at some rough checks to see if Anthony’s numbers were reasonable or not. Specifically, the returns he gives compound to reasonable annual performance so we don’t see any huge red flags right off the bat. I also discuss the importance of doing some “common sense” checking of ideas and results as a first step in any analysis.

We still have not yet addressed the most important questions which are: Is this a real edge? Is it tradable? What more would we need to know before risking money on it?

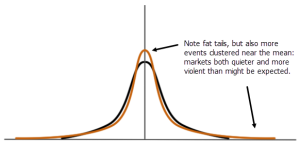What’s the baseline?

One of the critical things we should ask anytime we have a system or pattern is whether it makes enough money to be worth our time. To do this, one of the best comparisions is to look at the conditional returns (i.e., the returns after the pattern condition is triggered) against the unconditional returns (the “buy and hold” return, or if we simply entered on any random trading day). So this is the first piece of missing information we need to make an evaluation? What was the baseline return in Anthony’s sample?

Stocks tend to return about 7% a year, on average. Anthony’s test annualizes to between 3% and 5%, so it appears his pattern actually underperforms stocks in the long run. However, we do not know what time period he’s looking at. What if he generated these results over a period when the market was flat or down? If his particular “snapshot” of the market has a baseline return of -2%, then a +3% return is potentially very attractive. It is a good idea to consider results as excess returns, meaning:

Excess return = Conditional return – unconditional return

Excess returns may not tell the whole story, since we do need to know something about the magnitude of the baseline. For instance, a 2% excess if the baseline is 3% is possibly very different than if the baseline were 20%, but we’ll get to that in the next step.

How much variability?

When we see good results (whether in actual trading or backtesting) there’s a chance, of course, that we just got lucky. Significance testing is a statistical test that gives us some idea of how likely it is that the results we see are simply due to chance. We’re not going to dig into this too deeply here for a couple reasons. First, the techniques for conducting these tests are very well-known, but they require a decent background in statistics just to be sure you’re avoiding some common errors. Second, if you have that background you might not be out of the woods yet; though the procedures for calculating significance tests are not hard to learn, applying those tests to market data might be a bit of an art.

I think you should do some type of significance testing, but if you choose not to, then you at least need to look at some measure of variability of returns. Consider three situations:

• Your test shows 3% on average, with values spread evenly between 2% and 4%
• Your test shows 3% on average, with values spread evenly between 2% and 8%
• Your test shows 3% on average, with values spread evenly between -50% and +50%.

It should be pretty clear that these situations are probably very different. In the first, we could probably be reasonable sure that the 3% is a good representation of the data set, but in the last one, who knows? Standard deviation is one measure of variability, but also consider others like range, IQR, or actually looking at the distribution. It’s difficult to evaluate Anthony’s results without some understanding of variability.

Sample and sample size

Another thing to consider is what market data are you actually looking at? Recent data only? Old and recent data together? A short time period? Long? If you selected a short time period, was only one market regime represented? (For instance, tests on stock indexes using very recent data will probably show more mean reversion than we’d see over a larger sample.) If you carefully selected multiple regimes, have you imposed some structure on the data that might be unfair? Is it possible that you chose a data set that would be “good” for your test idea in some way?

Most people are comfortable with the idea of sample size–more is usually better–but even this relatively simple concept turns out to be not so simple. Did you run tests on a handful of stocks? How correlated are they? Did you include crude oil, rbob, and heat in the sample, and does that maybe introduce some relationships you should be aware of? How much data is too much? If you do this work, these are the kinds of questions you need to think about, and the answers will be a little bit different for different situations.

At the very least, be suspicious of very small sample sizes–I know blogs that point out things like “this condition has happened 6 times in the S&P 500 since 1980 and here’s a TradeStation system test showing what would have happened if you’d traded those patterns.” That’s not an edge–that’s usually a good example of fitting your conditions to the data so you can write a blog post. We need to know 1) how many datapoints in your dataset and 2) how many “trades” your system generates before we can start evaluating the idea.

Can I trade it and will it last?

Past performance is no guarantee of future results–we’ve all seen that tens of thousands of times, but it’s true. It’s true even in your own testing and work. Everything to this point has been designed to point us toward ideas that will be enduring. We can do some interesting things like slice our sample into different time periods, run the test on each period, and see if results are more or less stable. (Warning: issues of sample size will arise and it’s not so easy to answer the question of stability.)

We also need to consider economic significance. It’s certainly possible to find things that are statistically significant, i.e., they are “real” and even persistent in the data, but they are too small to trade. Some effects may not even come from actual trading–for instance, some markets may simply bounce between the bid and ask. If you’re looking at trade prices in this type of market (or, ugh, indexes that include instruments that may trade like this) then you have some complex microstructural issues to tease out. (Not to dodge the upcoming questions, but dealing with these issues requires a decent background in econometrics and understanding of market microstructure. This book will get you pointed in the right direction on the latter issues (and is a book I think every trader should read!))

Issues of test design

Even if we do everything correctly, there’s still a chance our test was flawed. A reader in a previous post pointed out, correctly, that you can generate guaranteed mean reversion with a random data set if you test for the maximum number of runs because, by definition, the next close will always reverse. You might also consider the difference between testing for N-length runs and runs of exactly N length. In the following data set {U, D, U, U, D, U, D, U, U, U, D} we might be inclined to think there are two separate runs (both bolded), one of N= 2 and one of N=3 length. However, if you aren’t careful your N=3 might include two N=2 runs. Is this what you wanted? Think carefully.

It would also be good to examine the results over a range of N’s. Anthony could re-run his test using N=1, N=2, etc.. We can think about what we might expect to see (smaller sample sizes with higher N’s and maybe larger effects) and then see what the data has to offer us.

In conclusion

These posts were fun to write, and I wanted to write an approachable guide to the thought process of analyzing trading ideas. More and more toolkits are available that allow traders to test ideas, but these are just tools. I can give you a $5000 camera or a $1000 knife, but that doesn’t mean you can take masterful pictures or cook a restaurant-quality meal. We have to know how to use the tools and develop the skills of using those tools.

Many of us find this work is fun and challenging, enormously frustrating at times, but even more rewarding at other times. I hope this post has given you some ideas, caused you to ask some questions, and perhaps even helps you a few steps along your own journey.