[dc]O[/dc]ne of the recurring themes of my writing is “be precise”. Too often we use concepts in ways that are not completely accurate, assuming that close is good enough, and that the lines on the screen tell a simple story. Sometimes this is true; sometimes it isn’t, but it is always important to truly understand the tools we are using. One of the most misused and abused concepts in the trading literature is correlation–traders usually assume that correlation is a measure of how two markets “move together”, but this is not exactly correct. For instance, consider the following chart of two theoretical data series. What would you assume the correlation is?
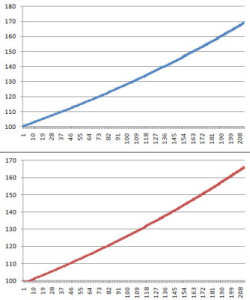
If you are like most people, you would probably assume that the correlation is something very close to 1.0. Most of us work with a simplistic understanding of correlation that runs something like this: correlation can range from 1.0 to -1.0. The closer to 1.0, the more they two data series “move together”; the closer to -1.0, the more likely they are to move in opposite directions. At a correlation of 0.0, there is no relationship between the two. Several months ago, tweeted this chart with the text: “Beware sloppy ‘correlation’ studies. You can’t tell by looking at charts. These two have a correlation of -1.0”, and was deluged with replies that basically said something like, “you’re wrong. You meant 1.0.” I replied to quite a few of the respondents, but I’m pretty sure that not a single of them believed I was anything but confused. Let’s zoom in and look at a section of the data a bit more closely:
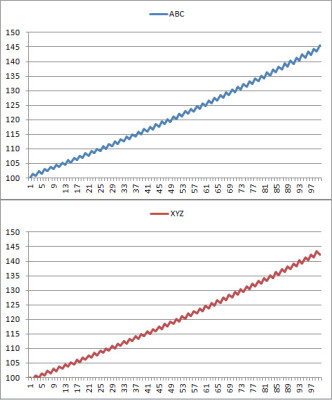
At this point, you can begin to see the trick. Series ABC moves in a pattern of +1.5%, -0.5%, +1.5%… Series XYZ uses the same pattern, but offset one day. In other words, Monday ABC has a return of +1.5%, and XYZ loses -0.5%. On Tuesday, ABC now goes down -0.5% while XYZ increases +1.5%. Over time, they both go up because they are gaining more than they are losing, but the correlation is exactly -1.0 because they are always moving in opposite directions on any given day.
Granted, this is a deliberately arcane and stylized example, but it makes an important point: Don’t assume that you can understand anything about the correlation between two markets by looking at a chart. It is so easy to find examples where the author is pointing to areas, saying “the correlation increased” in certain areas because the lines moved in the same direction. Maybe; maybe not.
at the time I thought this might be “the answer”. I have a question…would it be true that the daily correlation is -1 while the ,say, 1 month correlation is close to 1?
I think what you’re asking, in general, is would the correlation be different on different timeframes? The answer is almost always yes… and you are very much on the right track. (Sometimes the right questions show clearly that you’re thinking in the right directions!)